Math Section Strategies
Tips and strategies to help you succeed on the math portion of anlectrical aptitude test.
Overview
The math section of an electrical aptitude test typically covers several key areas:
- Algebra: Solving equations, working with variables, and manipulating expressions
- Functions and Graphs: Understanding function notation, graphs, and relationships
- Number Series: Identifying patterns and sequences
- Arithmetic and Mathematical Reasoning: Arithmetic and general problem-solving skills
General Math Strategies
- Don't leave any questions blank- at the 1-2 minutes remaining mark, start guessing
- Use your scratch paper- write out problems
- The time constraints are tight- don't spend too long on any single question. If you're stuck, make a note of the question number on your scratch paper, guess, and move on with the intention to come back. I recommend guessing and writing down the numbers in a special section of your scratch paper, that way you don't have to come back and guess but you still know which problem you haven't solved yet.
- If you're stuck, eliminate obviously wrong answers first. Some questions are best solved by checking every answer, especially complex factoring questions.
- Review your answers if time permits
Pattern Recognition
How to approach these problems
- I advise you to approach these problems in order of likelihood, the most likely pattern is addition / subtraction between adjacent numbers, so start there.
- Write out the differences / ratios between adjacent numbers and look for a pattern in those. Actually writing it out can help you see patterns.
- If addition and subtraction between the numbers does not yield a pattern, try multiplication and division between numbers, this is the next most likely pattern.
- If multiplication and division fail to reveal a pattern, try taking the square root or exponent of the numbers (one of the math practice problems uses square roots). These patterns are even less likely but it's good to have a system.
- If you're still stuck, try looking for a pattern in the numbers themselves. For example, if the numbers are all prime, maybe it's the next prime number in the sequence.
Worked examples
Try this pattern: What comes next in the sequence \(2,\,5,\,9,\,14,\,20,\,\ ?\)
Detailed explanation: Compute differences between numbers: \(5-2=3,\ 9-5=4,\ 14-9=5,\ 20-14=6\). Writing out the differences, we get \(3, 4, 5, 6\) and the pattern is more clear. The differences increase by 1 each time, so the next difference should be \(7\). Add it to the last term: \(20 + 7 = 27\). So the next term is \(27\).
Try this pattern: What comes next in the sequence \(3,\,5,\,2,\,6,\,1,\,\ ?\)
Detailed explanation: Compute differences between adjacent numbers: \(5-3=2,\ 2-5=-3,\ 6-2=4,\ 1-6=-5\). Writing out the differences, we get \(+2, -3, +4, -5\) and the pattern is more clear. The differences increase by 1 each time and alternate signs positive and negative, so the next difference should be \(+6\). Add it to the last term: \(1 + 6 = 7\). So the next term is \(7\). Alternatively, you could see the same pattern by seeing that every other number decreases by 1 (3, x ,2, y, 1) and the other numbers increase by 1 (5, m, 6, n, ?). These are different ways of seeing the same pattern.
Order of Operations, Algebraic Simplification, and Multivariate Formulas
How to approach Order of Operations and Multivariate Substitution problems
- These problems are order of operations / PEMDAS problems with extra steps of variable substitution.
- Make sure you understand and are confident with order of operations with numbers (math practice problems 61-65).
- Write out the problem on paper, substituting the values provided for the variables.
- Once it's written out, simplify one operation at a time in the correct order, just like an order of operations problem.
Worked example
Given: Evaluate
\[u = \frac{5v + 3w}{2v - w} \text{ where } v = 6 \text{ and } w = 2\]
- Substitute the values: \[u = \frac{5(6) + 3(2)}{2(6) - 2}\]
- Simplify the numerator: \[u = \frac{30 + 6}{2(6) - 2} = \frac{36}{2(6) - 2}\]
- Simplify the denominator: \[u = \frac{36}{12 - 2} = \frac{36}{10}\]
- Divide to get the final answer: Note: To divide or multiply any number by 10, move the decimal point one place left or right respectively- to the left for division and to the right for multiplication. \[u = \frac{36}{10} = 3.6\]
How to approach Algebraic Simplification problems
- Follow order of operations and try to go step by step
- If there are fractions, look to cancel out common factors in the numerator and denominator.
- Watch out for negative signs distributing to parentheses, for example \(-(x + y) = -x - y\) not \(-x + y\).
- Only combine like terms. Like terms must have the same variables with the same exponents. For example: \(3x + 5x = 8x\). However, \(3x + 5 \neq 8x\); \(4x^2 + 2x \neq 6x^2\); \(2xy + 3x \neq 5xy\); and \(5x - 3x^2\) cannot be combined because the exponents are different.
- Practicing these makes them easier to solve.
Worked example
Note that you are unlikely to see a problem this complex, regardless it's a good example of a lot of different algebra simplification skills. If you need easier problems to build up your skills or if this doesn't make sense, please check out some videos on simplifying algebraic expressions from a resource like Khan Academy or YouTube.
Given: Simplify the following expression.
\[ p = (4x^2 - 3xy + 6y) - \left(\frac{2x^2y - 4xy}{2x}\right) - \left(-3x + 2y\right) \]
-
Start with the fraction and look for terms that cancel.
Factor 2xy out of the numerator since both terms have that common factor: \[ \frac{2x^2y - 4xy}{2x} = \frac{2xy(x - 2)}{2x} \] Now cancel the common factor of \(2x\): \[ = y(x - 2) \] - Rewrite the original expression using the simplified fraction. \[ p = (4x^2 - 3xy + 6y) - y(x - 2) - (-3x + 2y) \]
-
Distribute the negative signs in front of the parentheses.
First distribute the minus sign to \(y(x - 2)\): \[ -y(x - 2) = -yx + 2y \] Next distribute the minus sign across the negative expression: \[ -(-3x + 2y) = +3x - 2y \] - Rewrite the expression with all terms expanded. \[ p = 4x^2 - 3xy + 6y - xy + 2y + 3x - 2y \]
-
Combine like terms.
Group similar terms: \[ p = 4x^2 - 4xy + 3x + 6y \] - Final Answer: \[ \boxed{p = 4x^2 - 4xy + 3x + 6y} \]
Variable Relationships
How to approach these problems
- These problems are pretty tricky, don't feel discouraged about them.
- Identify which variable is changing and which variable(s) are held constant.
- Pick a constant value, and write that in for the constant variable- now you have a 2d problem instead of 3d.
- Test the changing variable with two easy values (one smaller, one larger) while holding the constant fixed; compare the outputs.
Worked example
Given: With \(q\) held constant, how does \(r\) change as \(p\) changes in \[\displaystyle r = \frac{4p + 6}{p + q}\]
- Pick a constant: Let \(q = 3\). Then \[r = \frac{4p + 6}{p + 3}\]
- Test a smaller \(p\): If \(p = 3\), \[r = \frac{4(3) + 6}{3 + 3} = \frac{18}{6} = 3\]
- Test a larger \(p\): If \(p = 9\), \[r = \frac{4(9) + 6}{9 + 3} = \frac{42}{12} = 3.5\]
- Compare: As \(p\) increased from 3 to 9, \(r\) increased from 3 to 3.5, so \(r\) increases with \(p\) when \(q\) is held constant.
2D Graphing and Inequalities
How to approach these problems
- In my opinion the most reliable way to solve these problems consistently is to graph them. You can also plug in numbers to check the statements- both methods will be shown in the worked example.
- Don't let weird variables like p and q trip you up- they are no different than graphing x and y equations.
- First, solve the equation for one variable.
- Pick easy values (like 0, 1, or 2) for one variable and calculate the corresponding value of the other variable to find points on the line.
- Plot at least two points to visualize the line's direction and position.
- Use the graph to test each answer choice by checking if the given conditions make sense with the line's behavior.
Worked example
Given: Determine which statement is true for the equation
\[2m - 5 = 4n + 3\]
Answer choices:
A. If \(n\) is greater than 1, then \(m\) is greater than 8
B. If \(n\) is less than 0, then \(m\) is less than 4
C. If \(m\) is greater than 10, then \(n\) is negative
D. If \(m\) is less than 2, then \(n\) is greater than 1
Step 1: Solve for one variable and put it on the left hand side of equation, here we'll use \(m\)
Add 5 to both sides:
\[2m = 4n + 8\]
Divide both sides by 2:
\[m = 2n + 4\]
Step 2 (Note: skip this step if you are not graphing): Find two points to graph the line
Let's use \(n = 0\) and \(n = 1\) for easy calculations. Plug in those values for \(n\) to get the corresponding \(m\) values:
- When \(n = 0\): \(m = 2(0) + 4 = 4\), so the point is \((0, 4)\)
- When \(n = 1\): \(m = 2(1) + 4 = 6\), so the point is \((1, 6)\)
Step 3 (Note: skip this step if you are not graphing): Graph the line
- Plot the two points we calculated: (0, 4) and (1, 6). I like to use a table off to the side to write them down.
- Draw a straight line through the points.
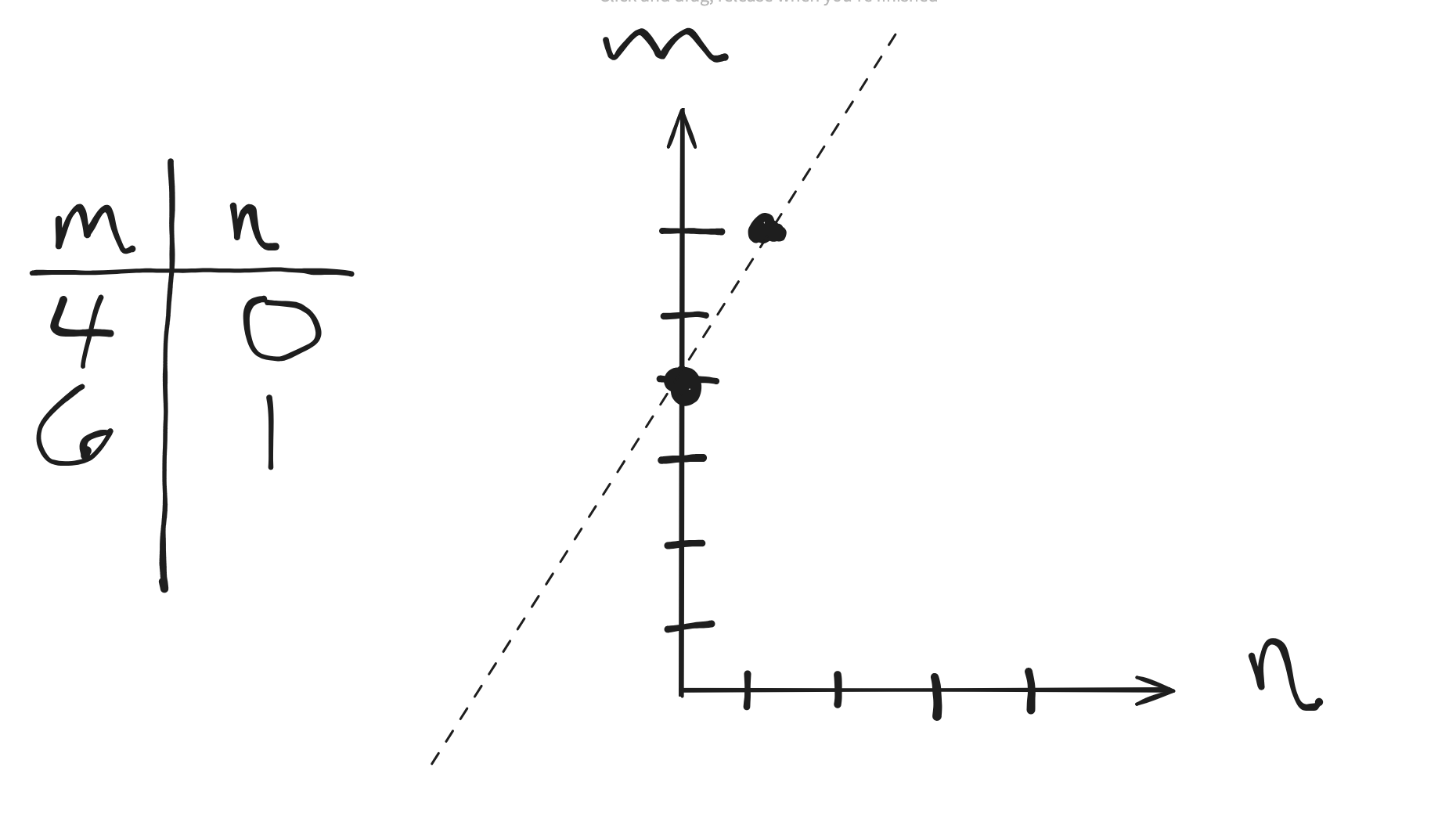
Step 4: Test each answer choice by either looking at the graph or plugging in numbers
Which of the following statements is true?
A. If \(n\) is greater than 1, then \(m\) is greater than 8
Test: If \(n = 1.5\), then \(m = 2(1.5) + 4 = 7\). Since \(7 < 8\), this is false.
B. If \(n\) is less than 0, then \(m\) is less than 4
Test: If \(n = -1\), then \(m = 2(-1) + 4 = 2\). Since \(2 < 4\), this is true.
C. If \(m\) is greater than 10, then \(n\) is negative
Test: If \(m = 12\), then \(12 = 2n + 4\), so \(2n = 8\) and \(n = 4\). Since \(4\) is positive, this is false.
D. If \(m\) is less than 2, then \(n\) is greater than 1
Test: If \(m = 0\), then \(0 = 2n + 4\), so \(2n = -4\) and \(n = -2\). Since \(-2 < 1\), this is false.
Answer: Only B is true. We can either plug in numbers to test, or look at the graph. It's a good idea to do both if time permits.
Factoring and Expanding
How to approach these problems
- For expanding: Use FOIL (First, Outer, Inner, Last) to multiply each term in the first parentheses by each term in the second parentheses.
- After FOILing, combine like terms carefully—watch the signs!
- For factoring: Sometimes it's easiest to FOIL each answer choice and see which matches the original expression. If this is slow for you, it may be a good idea to guess on these questions and come back if you have time.
Worked example: Expanding
Expand: \((3h - 2k)(2h + 5k)\)
Step 1: Apply FOIL
Multiply each term:
- First: \(3h \times 2h = 6h^2\)
- Outer: \(3h \times 5k = 15hk\)
- Inner: \((-2k) \times 2h = -4hk\)
- Last: \((-2k) \times 5k = -10k^2\)
Step 2: Write out all terms
\[6h^2 + 15hk - 4hk - 10k^2\]
Step 3: Combine like terms
Combine the \(hk\) terms: \(15hk - 4hk = 11hk\)
\[6h^2 + 11hk - 10k^2\]
Worked example: Factoring
Factor: \(6r^2 - 7rs - 3s^2\)
Answer choices:
A. \((3r + s)(2r - 3s)\)
B. \((2r + 3s)(3r - s)\)
C. \((6r + s)(r - 3s)\)
D. \((3r - s)(2r + 3s)\)
Step 1: Check choice A by FOILing
\((3r + s)(2r - 3s)\):
- First: \(3r \times 2r = 6r^2\)
- Outer: \(3r \times (-3s) = -9rs\)
- Inner: \(s \times 2r = 2rs\)
- Last: \(s \times (-3s) = -3s^2\)
\[6r^2 - 9rs + 2rs - 3s^2 = 6r^2 - 7rs - 3s^2 \quad \checkmark\]
This matches! Choice A is correct.
Step 2: Verify other choices (for practice)
Choice B: \((2r + 3s)(3r - s)\)
\[6r^2 - 2rs + 9rs - 3s^2 = 6r^2 + 7rs - 3s^2 \quad \text{(wrong sign on middle term)}\]
Choice C: \((6r + s)(r - 3s)\)
\[6r^2 - 18rs + rs - 3s^2 = 6r^2 - 17rs - 3s^2 \quad \text{(wrong coefficient)}\]
Choice D: \((3r - s)(2r + 3s)\)
\[6r^2 + 9rs - 2rs - 3s^2 = 6r^2 + 7rs - 3s^2 \quad \text{(wrong sign on middle term)}\]
Answer: Only choice A expands to \(6r^2 - 7rs - 3s^2\), so it is the correct factorization.
Multiple Representations
How to approach these problems
- Be familiar with types of graphs: Linear graphs are straight lines (equations like \(y = mx + b\)). Quadratic graphs are curved (equations with \(x^2\) terms). If there is a curved line, it is 'non-linear.' That means there is an exponent, root, absolute value, a trig function like sine or cosine, a variable times itself (same thing as an exponent), or a variable in the denominator of a fraction!
- Write out statements into formulas accurately. Read carefully: "y is x times itself" means \(y = x^2\), not \(y = 2x\).
- Plot 3 points to visualize the table or equation. If the line curves, it's non-linear. Since the graph may be non-linear (curved), it is important to check 3 points rather than 2!
- A systematic way to solve: Find three points from the given representation (statement, table, graph, or function) and check to see if they all exist on each answer choice. The correct answer will have all three points match.
Worked example
Problem statement: "y is x times itself plus two"
Step 1: Convert the statement to a formula
"y is x times itself plus two" means:
\[y = x^2 + 2\]
Step 2: Find three points to test
Let's calculate a few points from \(y = x^2 + 2\):
- When \(x = 0\): \(y = 0^2 + 2 = 2\), so the point is \((0, 2)\)
- When \(x = 1\): \(y = 1^2 + 2 = 3\), so the point is \((1, 3)\)
- When \(x = 2\): \(y = 2^2 + 2 = 6\), so the point is \((2, 6)\)
Step 3: Check each answer choice
Answer choices:
A. Table:
| \(x\) | \(y\) |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 5 |
| 3 | 10 |
Test: Our point \((0, 2)\) means that when \(x = 0\), \(y = 2\). This table should have \(y = 2\) when \(x = 0\), but it doesn't. Incorrect.
B. Graph 1:
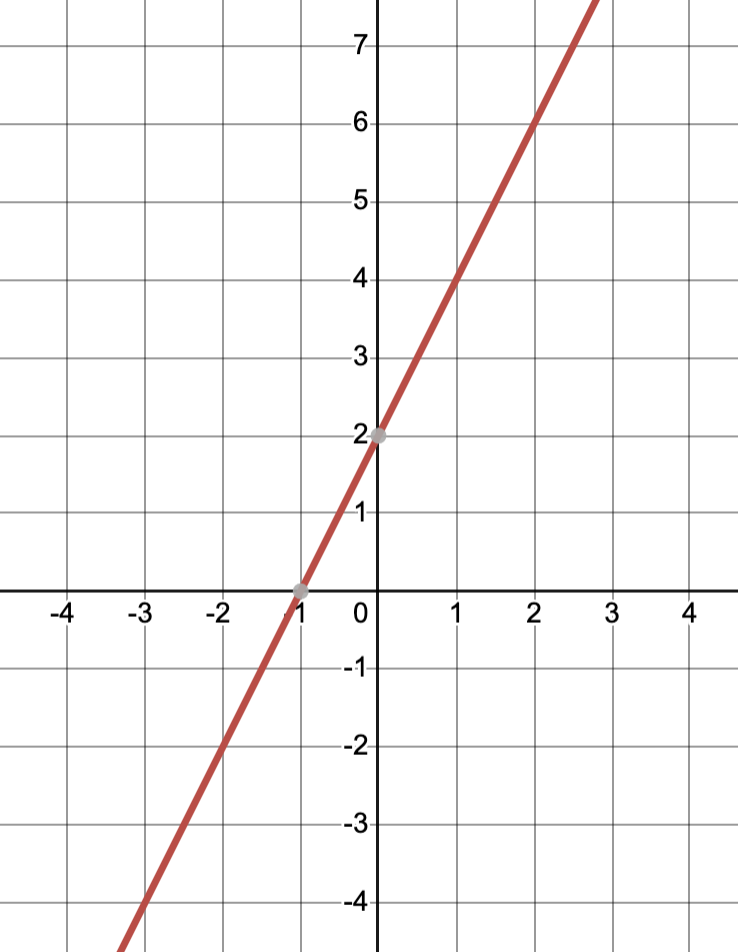
Test: Check if points \((0, 2)\), \((1, 3)\), and \((2, 6)\) are on this graph. Looking at the graph, we can see that the point \((1, 3)\) is not on the line. Since one of the points is missing, this graph is incorrect.
C. Graph 2:
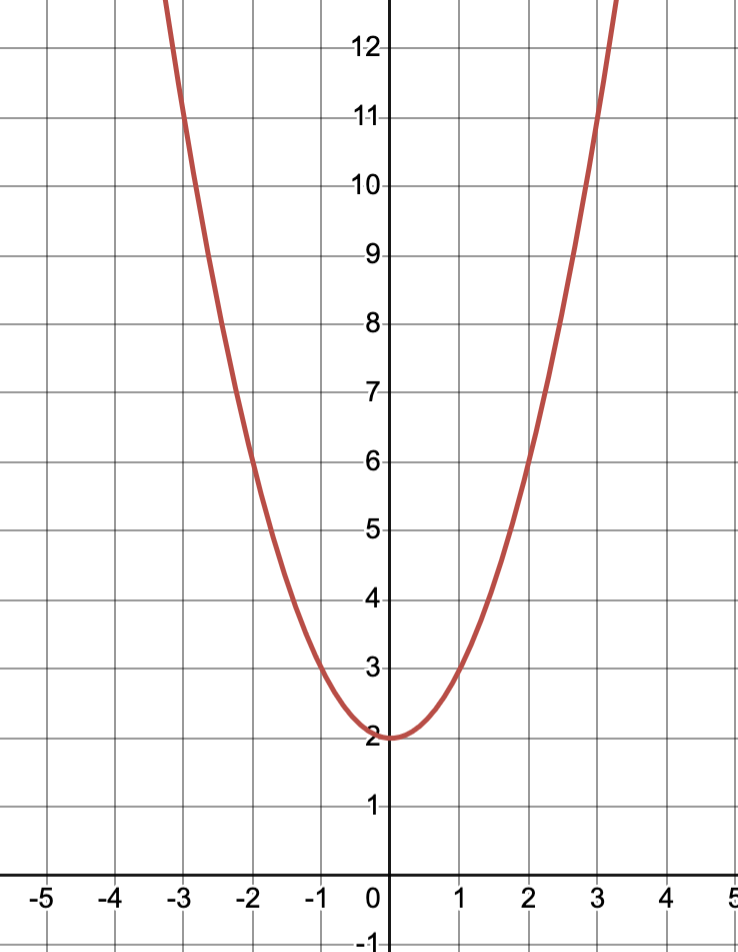
Test: Check if points \((0, 2)\), \((1, 3)\), and \((2, 6)\) are on this graph. All three points are. The graph is also curved, which is correct since we had an exponent in the equation. Correct.
D. Function: \(y = 2x + 2\)
Test: Check our points:
- \((0, 2)\): \(y = 2(0) + 2 = 2\) ✓
- \((1, 3)\): \(y = 2(1) + 2 = 4\) ✗ (should be 3)
- \((2, 6)\): \(y = 2(2) + 2 = 6\) ✓
Answer: Only Graph 2 (choice C) correctly represents \(y = x^2 + 2\). Notice that it's a curved line (parabola), which makes sense because the equation has an \(x^2\) term.
Fractions and Arithmetic
How to approach these problems
These problems test fundamental arithmetic skills. If you're struggling with fractions, decimals, long division, or multi-digit multiplication, the best approach is to use external learning resources to build these skills:
- Khan Academy: Excellent free video tutorials and practice problems for all arithmetic operations. Search for topics like "adding fractions," "multiplying decimals," or "long division."
- YouTube: Search for instructional videos on any specific topic you need help with. There are countless step-by-step tutorials available.
- AI Tools (ChatGPT, Claude, etc.): You can ask these tools to explain how to solve specific types of problems and walk you through examples step-by-step.
- Google Search: Simply searching for "how to add fractions," "how to multiply decimals," or "how to do long division" will return plenty of helpful articles, videos, and tutorials.
Once you understand the methods, practice is key. Use the practice problems on this site to test your skills (arithmetic problems are at the bottom), but don't hesitate to review the fundamentals using the resources above if needed.
Key concepts to master
- Fractions: Finding common denominators for addition/subtraction, multiplying numerators and denominators, dividing by multiplying by the reciprocal
- Decimals: Lining up decimal points for addition/subtraction, counting decimal places for multiplication
- Long Division: Breaking down the division process step-by-step
- Multi-digit Multiplication: Using the standard algorithm or distribution method