Math Practice
Practice math questions covering algebra, functions, number series, and mathematical reasoning.
Practice Instructions
- Work through each question at your own pace
- Focus on understanding the problem-solving approach
- Review explanations after answering (when available)
- Visit the Math Help page for tips and techniques
Pattern Recognition
Identify the pattern and determine the next number in each sequence.
Note: Some of these questions are harder than what you will see on the test. Try them, it's good practice!
1. What number comes next in this sequence?
\(1, 1, 2, 3, 5, 8, ?\)
2. What number comes next in this sequence?
\(1, 3, 3, 9, 27, 243, ?\)
3. What number comes next in this sequence?
\(10, 13, 11, 14, 12, ?\)
4. What number comes next in this sequence?
\(5, 8, 2, 11, -1, ?\)
5. What number comes next in this sequence?
\(1, 4, 9, 16, 25, ?\)
Multivariate Formulas
Substitute the given values into the formula and solve for the variable.
6. If
\[u = \frac{5v}{3w}\]
where \(v = 12\) and \(w = 5\), what is the value of \(u\)?
7. If
\[g = \frac{f^2}{5d}\]
where \(f = 8\) and \(d = 4\), what is the value of \(g\)?
8. If
\[e = \frac{\sqrt{4t}}{k/3}\]
where \(t = 16\) and \(k = 6\), what is the value of \(e\)?
9. If
\[i = \frac{7j}{4}\]
where \(j = 12\), what is the value of \(i\)?
10. If
\[e = \frac{5(t + 2)}{4k + w}\]
where \(t = 6\), \(k = 2\), and \(w = 6\), what is the value of \(e\)?
11. If
\[m = \frac{7n}{3p + q}\]
where \(n = 9\), \(p = 2\), and \(q = 3\), what is the value of \(m\)?
12. If
\[u = \frac{3v^2}{4w + z}\]
where \(v = 4\), \(w = 2\), and \(z = 4\), what is the value of \(u\)?
13. If
\[g = \frac{\sqrt{9f}}{d + h}\]
where \(f = 25\), \(d = 3\), and \(h = 2\), what is the value of \(g\)?
14. If
\[p = \frac{6(r - 3)}{2s + t}\]
where \(r = 11\), \(s = 3\), and \(t = 3\), what is the value of \(p\)?
15. If
\[x = \frac{8y + 4}{3z - w}\]
where \(y = 5\), \(z = 4\), and \(w = 2\), what is the value of \(x\)?
Variable Relationships
For each question, one variable is held constant. Determine how the dependent variable changes as the independent variable changes.
Note: These questions are really hard. If you're not getting them all, don't sweat it. Just do your best.
16. Given the formula
\[y = \frac{2z - x}{z} + 3\]
where \(x\) is greater than 1 and held constant, as \(z\) increases, what happens to \(y\)?
17. Given the formula
\[b = \frac{(a + 2)(c - 1)}{\sqrt{c}}\]
where \(c\ > 1\) and held constant, as \(a\) changes, what happens to \(b\)?
18. Given the formula
\[d = \frac{3e + f}{e - 2}\]
where \(f\) is held constant and \(e > 2\). As \(e\) increases, what happens to \(d\)?
19. Given the formula
\[h = \frac{\sqrt{k}}{k + j}\]
where \(j\) is held constant and \(k\) is positive. As \(k\) changes, what happens to \(h\)?
20. Given the formula
\[r = \frac{5s - t}{2s}\]
where \(t\) is held constant, as \(s\) increases, what happens to \(r\)?
2D Graphing and Inequalities
For each equation, determine which statement about the relationship between the variables is true. Graphing these problems is usually helpful.
21. Given the equation
\[4m = n + 8\]
which of the following statements is true?
22. Given the equation
\[3p = 2q - 6\]
which of the following statements is true?
23. Given the equation
\[5r = s + 10\]
which of the following statements is true?
24. Given the equation
\[2u = v - 4\]
which of the following statements is true?
25. Given the equation
\[6w = 3x + 12\]
which of the following statements is true?
Factoring
Expand the factored expressions or identify the correct factored form.
26. Expand:
\[(4g - 5n)(g + 2n)\]
27. Factor:
\[5p^2 - 8pq - 4q^2\]
28. Expand:
\[(5h - 3k)(h + 4k)\]
29. Expand:
\[(6m - 2n)(2m + 3n)\]
30. Factor:
\[7r^2 - 11rs - 6s^2\]
31. Expand:
\[(3t - 4u)(2t + 5u)\]
32. Factor:
\[8v^2 - 14vw - 15w^2\]
Multiple Representations
Match the given representation with the equivalent form from the answer choices.
33. The statement "y is 4 times x minus 2, all divided by x" is equivalent to which of the following?
34. The following table represents which relationship?
| \(x\) | \(y\) |
|---|---|
| -1 | 2 |
| 0 | 5 |
| 1 | 8 |
| 2 | 11 |
| 3 | 14 |
35. The following graph represents which equation?
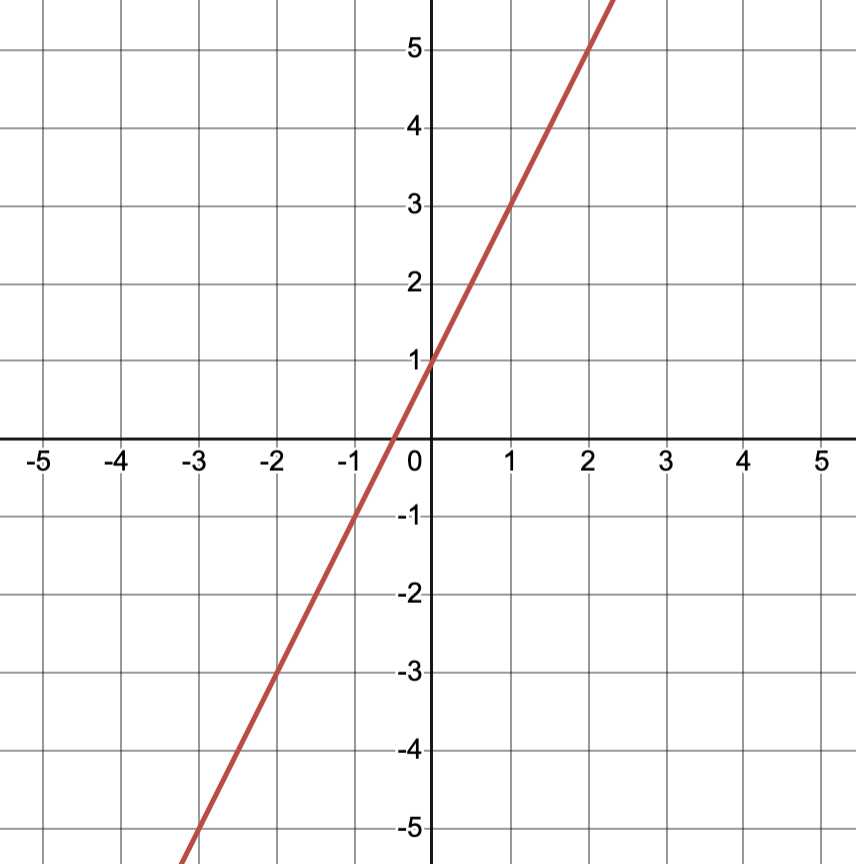
36. The equation \(y = 3x^2 - 7\) is best represented by which statement?
37. The statement "y is twice x plus 3" would produce a graph that:
Fractions
Add, subtract, multiply, or divide the following fractions and simplify your answer.
38. Add:
\[\frac{3}{8} + \frac{5}{12}\]
39. Add:
\[\frac{2}{5} + \frac{3}{7}\]
40. Add:
\[\frac{1}{3} + \frac{1}{4}\]
41. Subtract:
\[\frac{5}{6} - \frac{1}{4}\]
42. Subtract:
\[\frac{7}{8} - \frac{2}{5}\]
43. Multiply:
\[\frac{2}{3} \times \frac{5}{8}\]
44. Multiply:
\[\frac{3}{4} \times \frac{2}{5}\]
45. Divide:
\[\frac{3}{4} \div \frac{2}{5}\]
46. Divide:
\[\frac{5}{6} \div \frac{3}{4}\]
47. Divide:
\[\frac{7}{8} \div \frac{2}{3}\]
Arithmetic
Perform the following arithmetic operations.
48. Add: \(2.35 + 4.67\)
49. Subtract: \(8.47 - 3.29\)
50. Subtract: \(12.56 - 7.83\)
51. Divide: \(672 \div 14\)
52. Divide: \(855 \div 19\)
53. Divide: \(936 \div 13\)
54. Divide: \(1088 \div 16\)
55. Multiply: \(38 \times 45\)
56. Multiply: \(47 \times 52\)
57. Multiply: \(56 \cdot 43\)
58. Multiply: \((1.41)(6)\)
59. Multiply: \(2.35 \cdot 8\)
60. Multiply: \((3.27)(4)\)
Order of Operations
Evaluate each expression following the order of operations (PEMDAS: Parentheses, Exponents, Multiplication/Division, Addition/Subtraction).
61. Evaluate: \(((3 + 2)^2) - (8 \div 4) \times 6\)
62. Evaluate: \((24 - 6) \div (3 \times 2)\)
63. Evaluate: \((10 + 5) \times 2 - 12 \div 4\)
64. Evaluate: \((20 - 4) \div 2 + 3 \times 3\)
65. Evaluate: \(\sqrt{36} + (4 \times 2) - 5\)